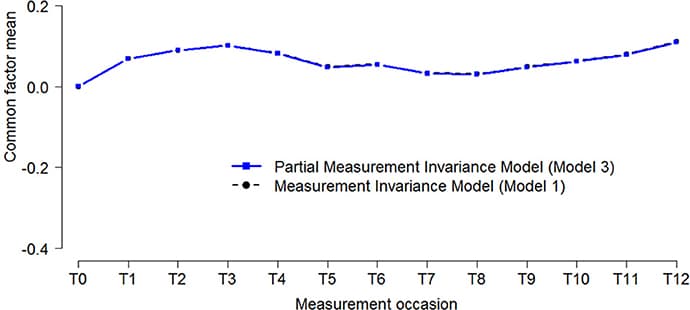
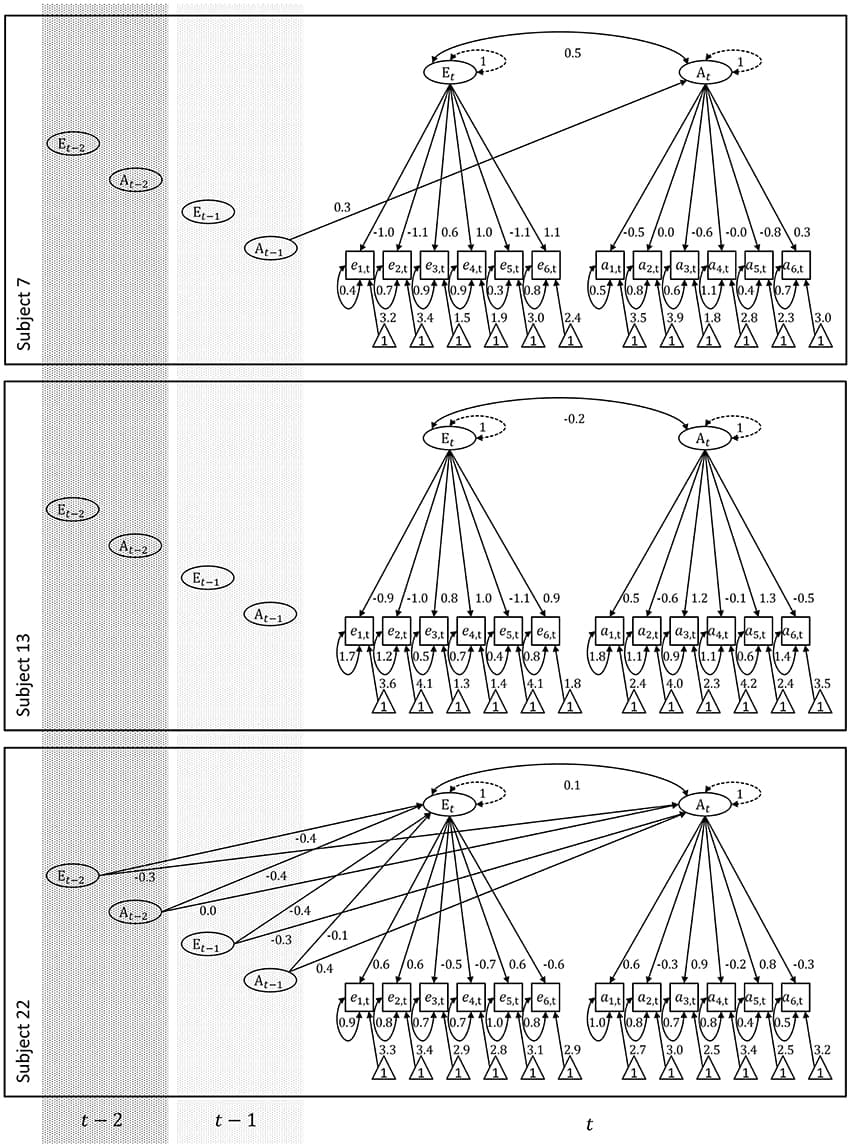
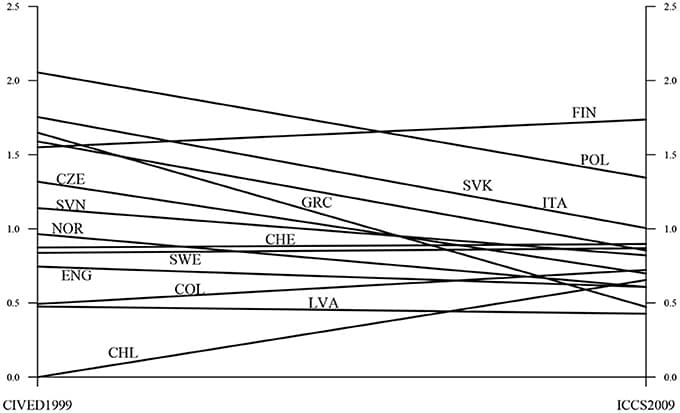
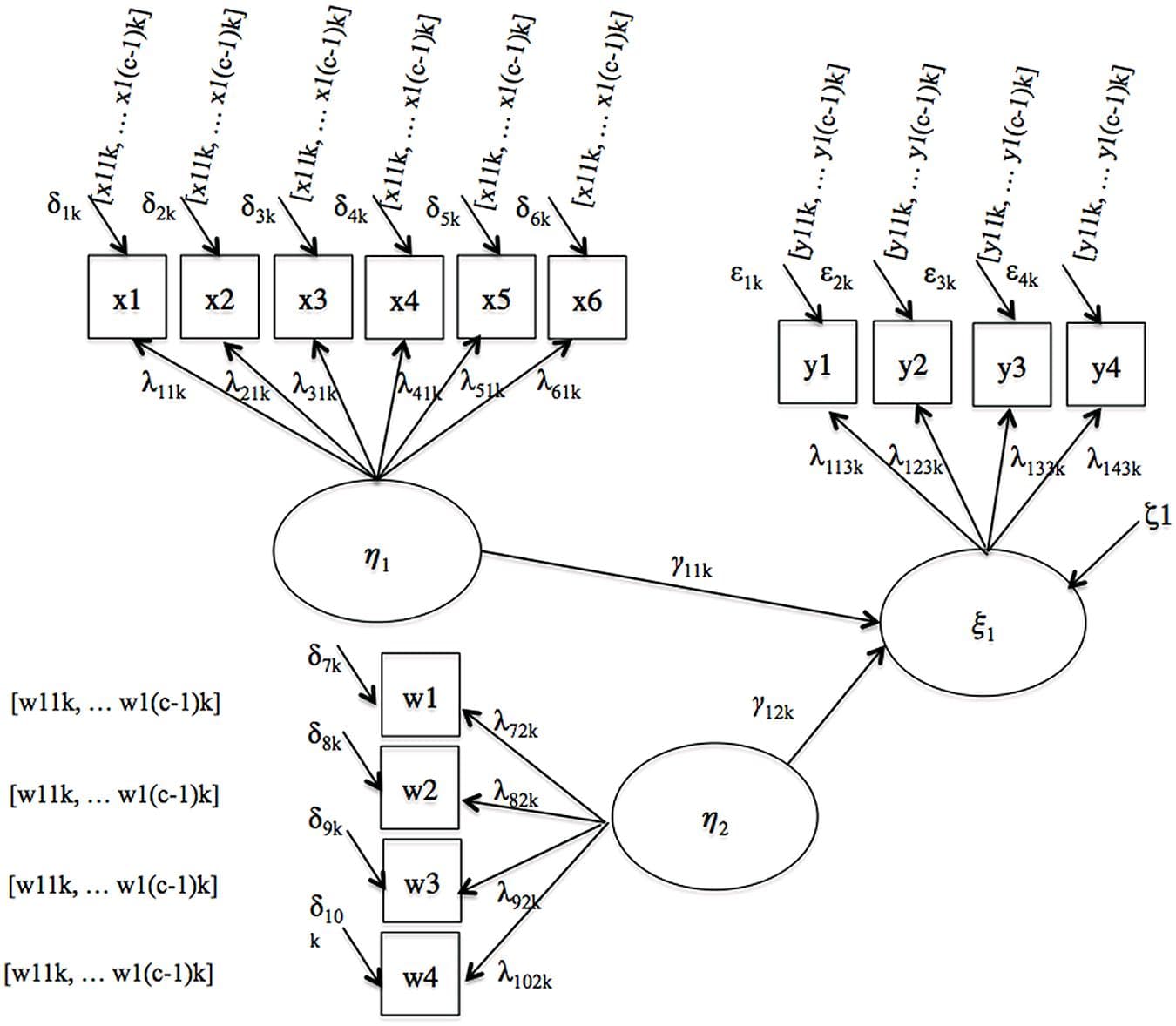
We address the question of equivalence between modeling results obtained on intra-individual and inter-individual levels of psychometric analysis. Our focus is on the concept of measurement invariance and the role it may play in this context. We discuss this in general against the background of the latent variable paradigm, complemented by an operational demonstration in terms of a linear state-space model, i.e., a time series model with latent variables. Implemented in a multiple-occasion and multiple-subject setting, the model simultaneously accounts for intra-individual and inter-individual differences. We consider the conditions—in terms of invariance constraints—under which modeling results are generalizable (a) over time within subjects, (b) over subjects within occasions, and (c) over time and subjects simultaneously thus implying an equivalence-relationship between both dimensions. Since we distinguish the measurement model from the structural model governing relations between the latent variables of interest, we decompose the invariance constraints into those that involve structural parameters and those that involve measurement parameters and relate to measurement invariance. Within the resulting taxonomy of models, we show that, under the condition of measurement invariance over time and subjects, there exists a form of structural equivalence between levels of analysis that is distinct from full structural equivalence, i.e., ergodicity. We demonstrate how measurement invariance between and within subjects can be tested in the context of high-frequency repeated measures in personality research. Finally, we relate problems of measurement variance to problems of non-ergodicity as currently discussed and approached in the literature.
Two major goals of this paper were, first to examine the cross-cultural consistency of the factor structure of the Hedonic and Eudaimonic Motives for Activities (HEMA) scale, and second to illustrate the advantages of using Bayesian estimation for such an examination. Bayesian estimation allows for more flexibility in model specification by making it possible to replace exact zero constraints (e.g., no cross-loadings) with approximate zero constraints (e.g., small cross-loadings). The stability of the constructs measured by the HEMA scale was tested across two national samples (Polish and North American) using both traditional and Bayesian estimation. First, a three-factor model (with hedonic pleasure, hedonic comfort and eudaimonic factors) was confirmed in both samples. Second, a model representing the metric invariance was tested. A traditional approach with maximum likelihood estimation reported a misfit of the model, leading to the acceptance of only a partial metric invariance structure. Bayesian estimation—that allowed for small and sample specific cross-loadings—endorsed the metric invariance model. The scalar invariance was not supported, therefore the comparison between latent factor means was not possible. Both traditional and Bayesian procedures revealed a similar latent factor correlation pattern within each of the national groups. The results suggest that the connection between hedonic and eudaimonic motives depends on which of the two hedonic dimensions is considered. In both groups the association between the eudaimonic factor and the hedonic comfort factor was weaker than the correlation between the hedonic pleasure factor and the eudaimonic factor. In summary, this paper explained the cross-national stability of the three-factor structure of the HEMA scale. In addition, it showed that the Bayesian approach is more informative than the traditional one, because it allows for more flexibility in model specification.
Measurement invariance (MI) is a pre-requisite for comparing latent variable scores across groups. The current paper introduces the concept of approximate MI building on the work of Muthén and Asparouhov and their application of Bayesian Structural Equation Modeling (BSEM) in the software Mplus. They showed that with BSEM exact zeros constraints can be replaced with approximate zeros to allow for minimal steps away from strict MI, still yielding a well-fitting model. This new opportunity enables researchers to make explicit trade-offs between the degree of MI on the one hand, and the degree of model fit on the other. Throughout the paper we discuss the topic of approximate MI, followed by an empirical illustration where the test for MI fails, but where allowing for approximate MI results in a well-fitting model. Using simulated data, we investigate in which situations approximate MI can be applied and when it leads to unbiased results. Both our empirical illustration and the simulation study show approximate MI outperforms full or partial MI In detecting/recovering the true latent mean difference when there are (many) small differences in the intercepts and factor loadings across groups. In the discussion we provide a step-by-step guide in which situation what type of MI is preferred. Our paper provides a first step in the new research area of (partial) approximate MI and shows that it can be a good alternative when strict MI leads to a badly fitting model and when partial MI cannot be applied.